粒子ボリュームレンダリング─理論とプログラミング
まえがき
- 1988年にSIGGRAPHで,可視化技術であるボリュームレンダリングについての講演が発表された.
- 3次元グラフィックスにおいて画像を生成する処理の名称「レンダリング」に,空間を表す「ボリューム」が結合されたのである.
- 芸術が科学技術の進歩を促した一例.
- ボリュームレンダリングでは,重要なデータに対して不透明度を高めていく作業において,与えられたボリュームデータの特徴を抽出する処理は大変重要な役割を果たす.
- ボリュームデータは,格子と呼ばれる空間を分割した小立体ごとに定義される場合がほとんどである.
- 特徴抽出は格子ごとに行うことが多い.
- ボリュームレンダリングは,現在,拡張性の観点で大きな壁にぶつかっている.ボリュームデータの規模が大きい場合,なんらかの形でモデル領域の分割を行い,並列計算技術を使用して計算機処理をする.
- ボリュームレンダリングでは,すべての格子を視点からの距離に応じてソートする処理が必要となる.そのため,領域分割が複雑な場合,ソート処理自身が不可能になる場合もある.
- 本書で扱う粒子ボリュームレンダリングは,ボリュームレンダリングをソート処理の呪縛から解放する画期的な手法である.
- 面や線といった3次元シーンの構成要素を適切に粒子表現すれば,ボリューム・面・線によって表現されるシーンの統合的レンダリングが可能となる.
1.可視化概要
- 本書では,ボリュームデータとして,3次元格子で定義された数値データを取り上げる.
- 人間の脳神経細胞の約半分は視覚と関係しており,可視化はそのような脳神経細胞を活性化する役割を担うもの.
- 可視化の研究領域においては三つの問題が指摘されている.
- 一つ目は,大規模データを処理する必要性.
- 二つ目は,視覚的コミュニケーションの必要性.
- 三つ目は,計算の操縦についての必要性.
- 1987年に,SIGGRAPHで等値面表示"マーチングキューブ法"に関する講演.
- 1988年に,SIGGRAPHでボリュームレンダリングに関する講演.
- 情報過多によって,poverty of attention(注目の貧窮)に陥らないようにするために,可視化技術の担う役割は大きい.
- ボリュームレンダリングの大きな魅力は,一つのピクセルに多くの情報を重畳(ちょうじょう)できるという点.
- 従来のボリュームレンダリングでは,すべての格子を平等に取り扱ってきた.ここに問題の原因が潜んでいると考え,本書で解説する粒子ベースアプローチでは,ボリュームデータの特徴を抽出し,ボリュームデータに集中と選択の戦略を取り入れる.重要な粒子からは多くの情報を,そうでない粒子からは少ない粒子を発生させ,手元のパソコンで対話的に表示させようというものである.
2.ボリュームデータ
- 数値データは大きく分けてスカラ・ベクトル・テンソルに分類できる.
- スカラデータは,大きさだけを持ち,方向に関する情報は持たない.
- ベクトルデータは,大きさ及び方向に関する情報をもつ.
- コンピュータグラフィックスにおける幾何形状の処理において,任意の多角形を三角形分割することが多い.三角形は他の多角形と違い,平面であることが保証されるので処理の上で取り扱いが容易となり,したがって計算コストの削減にもつながる場合がある.
- 四面体格子データを使えば,ボリュームレンダリングで必要な視線探索を効率良く行うことができる.
3.データ処理
3.1 データ補間
- ボリュームデータでは数値データが定義されているのは離散点であり,データ値が必要とされる点とは一致しない.
- ボリューム可視化では,データ値が必要とされる点を含む格子を探索し,その格子の節点で定義されたデータ値を用いてデータ値の補間を行う.
3.2 格子における特徴探索
- 格子内部のデータ分布について,補間関数を用いて陽的(y=f(x)の形)に表現することができれば,格子単位で,極点・特異点・縮退点といった特徴を抽出することが可能となる.
- 極点は,スカラ場においてその勾配が0となる点である.
- 特異点は,ベクトル場においてベクトルデータが0となる点である.
- 縮退点は,テンソル場において,テンソルデータを固有値分解して得られる固有値のうち二つまたは三つが同じ値をとる点である.
4.ボリュームレンダリング
- ボリュームレンダリングは,対象とするボリュームデータを半透明の雲のように表現することによってデータの内部構造を含めた全体的な特徴をうまく表現する可視化手法である.
- 1988年にSabellaによって提案された手法では,スカラボリュームの可視化を目的として,粒子を反射体ではなく放射体として扱う(粒子発光モデル)ことによって,ボリュームデータの内部構造を分かりやすく表現するための手法を提案した.
- 実際にボリュームデータをディスプレイに表示するためには,視点と画素を結ぶすべての視線に対して,輝度値を計算する必要がある.(図4.5)
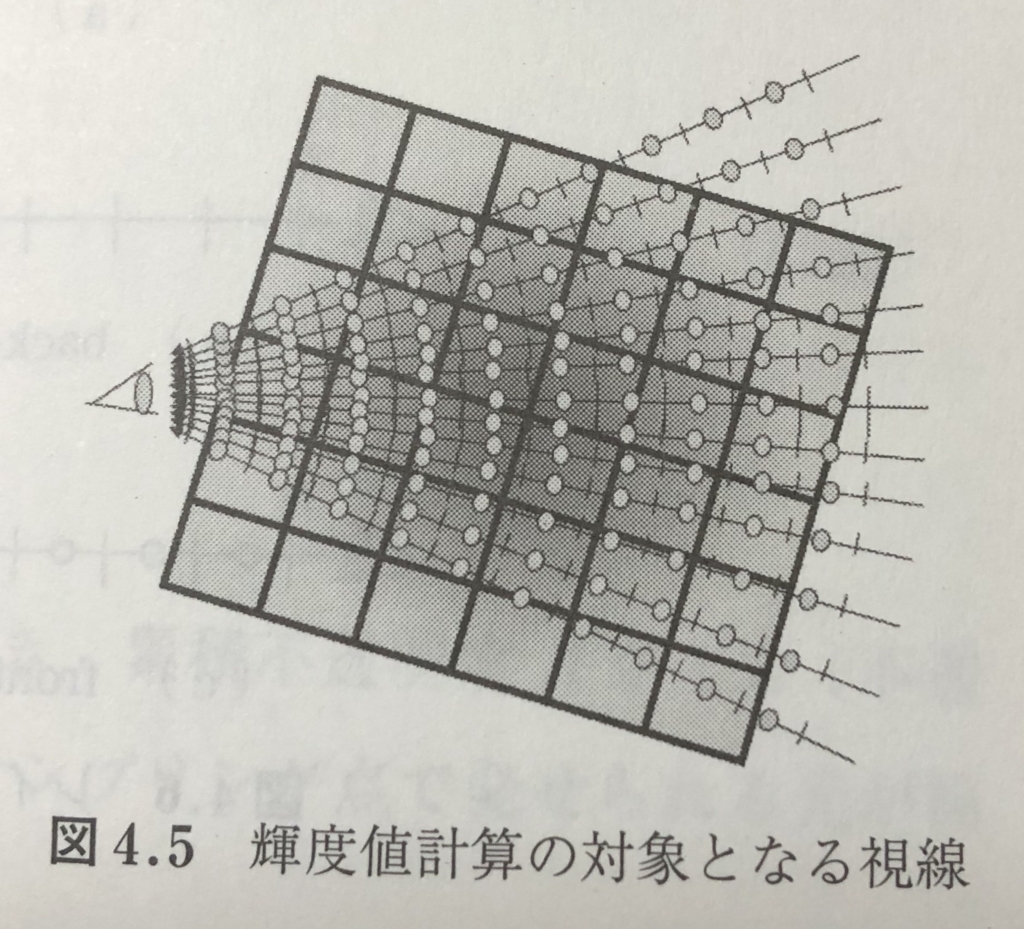
5.粒子ボリュームレンダリング
5.1 ソート処理からの決別
- ボリュームレンダリング法として広く利用されている格子投影法やその高精度版である事前積分法については,視点位置が変更されるごとに格子のソート処理が必要であり,大規模・複雑ボリュームデータを対象とする場合には,処理時間とその処理に必要とされるメモリ量の膨大さのために実行困難または実行不能な状況が発生する.
- レイキャスティング法はとりわけ大規模なボリュームデータに対しても有効であるが,ピクセルより小さいサイズの重要な四面体からの寄与を無視する可能性がある.また,隣接格子情報を必要とし,必要メモリの増大につながる.
- これらの問題の原因は,ボリュームデータを半透明属性を持つ連続体で表現していることにあり,問題の解決には根本的な手法の見直しが必要である.
- → モデルの再検討をする.
→ 現在のボリュームレンダリングの計算モデルでは,まず,密度分布を持つ不透明な発光粒子群という離散モデルとして表現された3次元空間において,光の振る舞い(発光・吸収)を考察.
→ 次に,発光粒子の密度を属性とする連続体としてボリュームデータをモデル化している.(離散モデルから導出された連続体モデル) - このボリュームレンダリング用連続体モデルで輝度値計算を行うためには,視線上でのサンプリング点から視点までの区間において粒子密度を積分する.(前回の積分結果を再利用する.)
- この場合,サンプリング点について視点からの距離を基準としたソートが必要となり,ボリュームデータが大規模・複雑化した場合,これがボトルネックとなる.
- この問題を解決するために,ボリュームレンダリング用連続体モデルが導出された離散モデルへの回帰を試みる.すなわち,粒子発光モデルに従って,確率論的アプローチによりボリュームデータ内部に不透明属性を持つ発光粒子を生成し,ボリュームデータをこれら不透明発光粒子集合という離散モデルとして表現することにより,この問題を解決しようとするもの.
- PBVRでは,ボリュームレンダリングの重要な特徴である半透明効果を実現するために,最終画像生成局面において輝度値のアンサンブル平均化処理を行う.
- PBVRでは,粒子をソートする必要がなく,画素単位に投影された複数粒子の平均化処理を行うだけでよい.
5.2 処理概要
- PBVRは,基本的に,粒子生成・粒子投影という2つの処理ステップから構成されるシンプルな手法である.
- 粒子生成前には,粒子密度の推定が必要であり,不透明度に関するユーザ指定の伝達関数から式にしたがって粒子密度関数を求める.
5.3 粒子密度推定
- 不透明度は,粒子の密度と正の相関がある.(粒子密度が高いと,不透明度が高くなる)
- 粒子密度推定の精度ということでは,同じ伝達関数を用いて作成したレイキャスティングによるボリュームレンダリング画像と同じ画像を作成できるかどうかで決定する.
5.4 粒子生成
- 導出した粒子密度推定式を用いて,ボリュームデータを構成する格子ごとに粒子生成を行う.
5.6 粒子投影
- 生成された粒子の投影処理では,Z-バッファアルゴリズムを使って視点に最も近い粒子の投影像を残し,それらを使って画素値を計算する.
- 粒子は不透明なので,視点からの距離に応じたソートが不要.
- 繰り返しを増やせば増やすほど画質は向上する.
6.3次元グラフィックス基礎
7.可視化プログラミングの基礎
7.1 可視化プログラミング
- ボリュームデータを可視化する場合,いったん幾何データに変換してから描画する方法(間接法)と,直接画像データを計算する方法(直接法)が考えられる.
- 間接法では,いったん幾何データに変換された数値データについては,標準的なグラフィックスAPIを利用することで,座標変換および陰影処理を固定的に適切な順序で高速実行することができる.
- 直接法では,描画段階においてデータ処理を行い,座標変換および陰影処理を独自に実装する必要がある.
- ボリュームデータは格子形状の違いにより規則格子データ,構造格子データ,不規則格子データに分類することができる.
- 粒子ベースボリュームレンダリングであれば,格子形状によらず,格子ごとのデータ処理が可能であれば,どのような格子形状であっても描画することができる.
- 不規則格子データを表すオブジェクトクラスが持つ属性を以下に示す.
・格子タイプ(cellType):格子の形状(四面体・六面体など)
・格子数(ncells):格子の数
・節点数(nnodes):節点の数
・節点座標(coords):節点の座標値配列
・数値データ(values):数値データ配列
・数値データのベクトル長:1の場合スカラ,3の場合ベクトルを表す.
・接続情報(connections):格子を特定するための節点番号配列 - KVSでは,不規則格子データはkvs::UnstructuredVolumeObjectクラスとして実装されている.
- 可視化パイプラインを構成する処理ステップは,フィルタリング,マッピング(粒子生成),レンダリング(粒子投影)の三つの処理に分類される.
[1]フィルタリング
可視化対象となるデータの変換を行う処理である.
[2]マッピング
ボリュームデータに対して色情報を割り当て,幾何データに変換する処理である.色情報の割り当てには伝達関数を利用する.つまり,マッピング処理は,伝達関数を利用した「ボリュームデータから幾何データへの変換処理」であるといえる.
[3]レンダリング
ボリュームデータまたは幾何データから画像データを生成し,ディスプレイに表示する処理である.つまり,レンダリング処理は,「ボリュームデータまたは幾何データから画像データへの変換処理」であるといえる.幾何データから画像データへの変換処理は,グラフィックスカードが標準的にサポートしている処理である.一方,ボリュームデータを直接画像化するボリュームレンダリングにおいては,数値データに対応する色と不透明度を伝達関数から算出し,それらを適切な順序で計算することによって画素値を計算し,最終画像を生成する処理を独自に実装する必要がある.
7.2 フィルタリング・マッピング処理の要素技術
- マッピング処理においては,数値データ(スカラ値)から色と不透明度への変換を行う伝達関数の設計が,意味ある可視化画像を生成する上で重要な役割を果たす.
- 伝達関数は,横軸にスカラ値をとり,縦軸に色または不透明度をとる関数として表現される.
- 伝達関数を適切に設定することによって,ボリュームデータの特定領域の強調や分類といったことが可能となる.
- 医療分野でのCTやMRIから構成されるボリュームデータを対象にした可視化では,例えば,骨を表す領域に対しては白,皮膚を表す領域に対しては黄色,血液を表す領域に関しては赤というような色を割り当てることによって実物に近い可視化結果を得ることができる.
- また,骨を表す領域に対しては不透明度を高くし,その他の部分は不透明度を低くすることで,骨部分を強調した可視化結果を得ることができる.
- 伝達関数の調整は,可視化結果に大きく影響する操作であり,ボリュームデータの特徴やデータ内部で生じるさまざまな変化を適切に描画するための重要な技術の一つであるとされる.
7.3 レンダリング処理の要素技術
- レンダリング処理は,幾何データまたはボリュームデータを画像データに変換する処理であり,OpenGLやDirectXといったグラフィックスAPIを利用して実装されることが多い.
- GPUは,3次元データを2次元画像へ変換する作業を,並列処理によって効果的に実行できるよう設計されている.
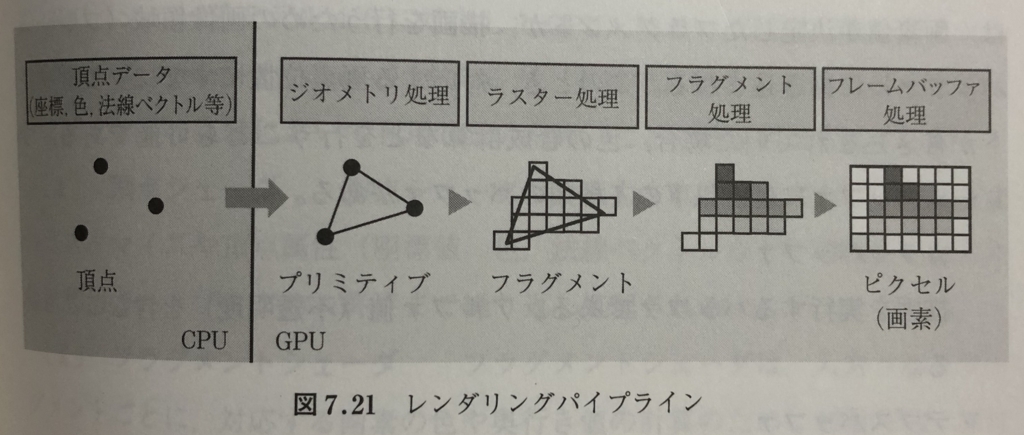
- GPU上で実行されるレンダリングパイプラインでは,対象となる3次元データを構成する頂点データ(座標値,色,法線ベクトルなどの情報を含む)を,OpenGLやDirect3Dに代表されるグラフィックスライブラリを利用してGPUに転送し,以下に示す4つの処理ステージを経て,最終画像をディスプレイに表示する.
[1]ジオメトリ処理ステージ
ジオメトリ処理ステージでは,GPUに転送されてきた頂点データに対して,回転・平行移動・縮小/拡大などを行う.この処理では,頂点データに対して座標変換処理が行われ,オブジェクト座標からスクリーン座標への変換が行われる.
[2]ラスター処理ステージ
ラスター処理ステージでは,プリミティブをフラグメント集合に変換する.各フラグメントは,スクリーン上の画素に対応している.
[3]フラグメント処理ステージ
フラグメント処理ステージでは,フラグメントに対して,プリミティブの各頂点の属性から補間計算が行われ,最終的な画素値が計算される.
[4]フレームバッファ処理ステージ
フレームバッファ処理ステージでは,画素値が決定したフラグメントが,描画を行うための画像領域(フレームバッファ)に書き込まれる.このとき,対応する画素位置にすでにフラグメントが書き込まれていた場合,色の合成計算など行うことも可能である.
- フレームバッファには,以下の4種類のバッファがある.
・カラーバッファ
描画を実行するバッファである.アルファ値(不透明度)を含むこともある.
・デプスバッファ
各ピクセルのデプス値を保存するバッファである.デプスバッファはZバッファと呼ばれることもあり,奥行き比較などにも利用される.
・ステンシルバッファ
画面の特定領域に描画を制限するようなマスキング処理に利用されるバッファである.
・アキュムレーションバッファ
画像の蓄積のためのバッファである.シーンのアンチエイリアス処理などに利用される. - 現在のレンダリングパイプラインでは,頂点変換処理の書き換えを可能とする頂点シェーダ(vertex shader)と,フラグメント処理の書き換えを可能とするフラグメントシェーダ(fragment shader)が利用できる.
[1]頂点シェーダ
頂点シェーダは,入力される頂点ごとに,変換方法のカスタマイズや頂点属性(座標値,色,法線ベクトルなど)の修正を行うため利用され,プログラム終了まで繰り返し処理される.
[2]フラグメントシェーダ
フラグメントシェーダは,入力されるフラグメントごとに,対応する画素の色や奥行き値の計算のために利用され,プログラム終了まで繰り返し処理される. - シェーダを利用して高速なレンダリングを実現するためには,対象とするデータを格納するためのGPU上のメモリ領域が必要となる.最近のGPUであれば,テクスチャ,頂点バッファオブジェクト(VBO:vertex buffer object),フレームバッファオブジェクト(FBO:framen buffer object)などが利用可能である.
[1]テクスチャ
テクスチャは,ポリゴンにテクスチャマッピングを行う際に,画素データ格納しておくための領域である.
[2]頂点バッファオブジェクト
頂点バッファオブジェクト(VBO)は,頂点データ配列をまとめてGPU上に格納するための領域である.
[3]フレームバッファオブジェクト
フレームバッファオブジェクト(FBO)は,あらかじめ定義されている表示ウィンドウ向けのフレームバッファとは別に,2次元配列データを格納することができる. - 粒子ボリュームレンダリング(PBVR)は,ボリュームデータ内部に粒子を生成し,その生成された粒子を単純に描画する手法である.
- 粒子生成処理はCPU上で行い,生成された粒子をGPUに転送し描画を行う戦略をとる.
- 生成された粒子は,頂点データとして表されているため,VBOに直接格納することができる.
8.粒子ボリュームレンダリングソフトウェア
- PBVRは,ボリュームデータ内に利用者が指定する伝達関数から求めることができる粒子密度を満足するように不透明粒子を生成し,それらの粒子をそのまま描画する方法である.
8.1 可視化パイプラインの構成
- 粒子生成処理は,ボリュームデータを入力として,ユーザ指定の伝達関数をもとにして粒子密度を推定し,格子単位で粒子(幾何データ)を生成する処理である.
8.2 粒子生成モジュールの実装
- 粒子生成処理は,以下の三つの処理ステージから構成される.
1.ユーザ指定の伝達関数から粒子密度を推定する.
2.推定された粒子密度から生成すべき粒子数を決定する.
3.粒子を生成する.

- 格子内に生成する粒子の数を推定するためには,粒子密度を計算する必要がある.
- 格子に含まれる節点上のスカラ値を平均することによって格子中心位置でのスカラ値を求め,その値に対する不透明度から粒子密度を計算する.そして,計算された粒子密度に格子の体積を掛けることで粒子数を求めることができる.
- KVSのGenerateParticlesInCellは1格子内での粒子生成処理関数を表しており,一様サンプリング法,棄却サンプリング法,メトロポリスサンプリング法のいずれかを表している.
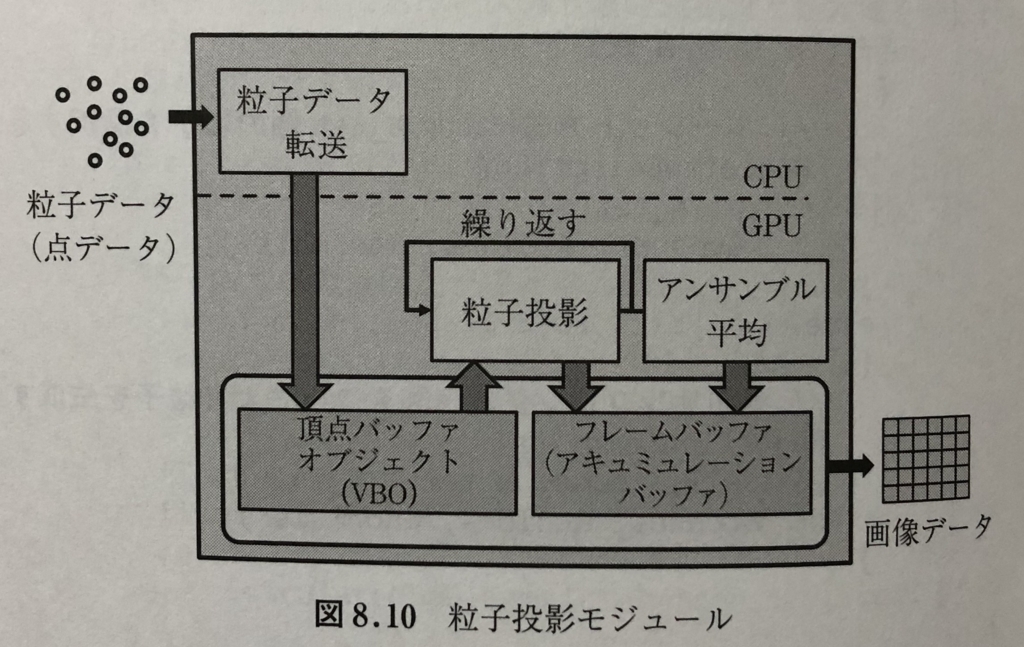
8.3 粒子投影モジュールの実装
- 粒子投影処理は,生成された粒子をZ-バッファアルゴリズムを利用して投影し,投影される粒子に対してシェーディング計算を行った後,アンサンブル平均処理によって最終画素値を決定する処理である.
- このレンダリング処理モジュールは,以下の三つの処理ステージから構成される.
1.粒子データをGPUに転送する.
2.粒子データを投影する.
3.アンサンブル平均処理を行う.
- VBOに格納されている粒子データを投影する際に,頂点シェーダ内で視距離に応じた粒子投影像の大きさを適切に計算し描画することで拡大操作にも対応した処理を行う.
- フラグメントシェーダ内では,粒子の投影像を円として描画する処理とシェーディング処理を行う.
- マウスの操作中はリピートレベルを1でレンダリングを行い,静止したところで繰り返し回数を増やしてレンダリングを行うことによって,対話性の高い効果的な可視化を行うことが可能である.
- PBVRでは,粒子投影処理を以下のように分類する.
[初期化処理]
・粒子データ転送(DownloadParticles)
・シェーダ初期化(InitializeShader)
[描画処理]
・アンサンブル平均化処理(EnsembleAverage)
・粒子投影(ProjectParticles)
本レンダリング処理モジュールの具体的な実装については,KVSのkvs::glew::ParticleVolumeRendererクラスを参照.
