PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation

Paper（6100 words, CVPR2017）

stanford.edu

f:id:tom0930:20190509233152p:plain

Source Code

github.com

Abstract

点群は重要な幾何学的データ構造である．
点群は（画像とは異なり）不規則な構造であるため，ボクセルグリッドまたは画像の集合に変換する処理をおこなうのが一般的．
しかし，これはデータを不必要に増大させ，多くの問題を引き起こす．
本論文では，点群データを直接入力とする新しいタイプのネットワークを設計した．
提案手法は，入力点群における点の順不同に配慮している．
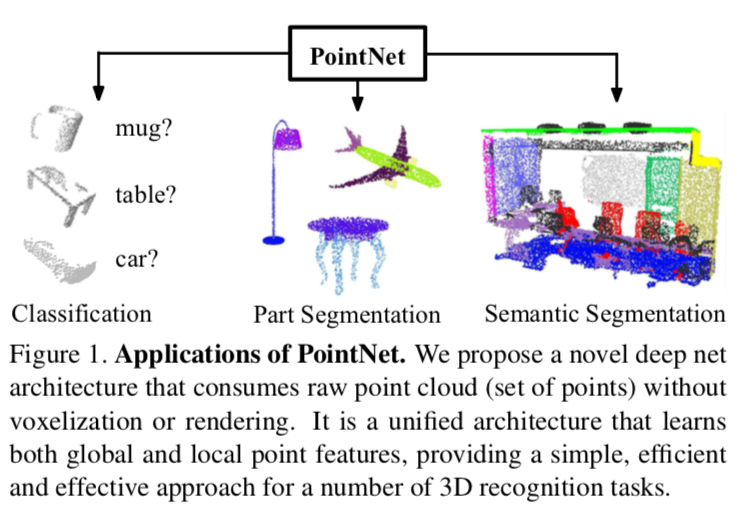
提案手法「PointNet」は，オブジェクトの分類，部分のセグメンテーション，シーンの意味解析への応用のための統一されたアーキテクチャを提供する．
シンプルではあるが，PointNetは非常に効率的かつ効果的である．
経験的に，最先端技術と同レベルあるいはそれ以上の，高いパフォーマンスを示している．
PointNetが「何を学習するのか」ということと「なぜ入力データに対してロバストなのか」ということに対する理論的な分析をおこなう．

1. Introduction

本論文では，点群やメッシュのような３次元幾何学データを推論することができるディープラーニングアーキテクチャを調査する．
一般的な畳み込みアーキテクチャは，重み割当やカーネル最適化をおこなうために，画像やボクセルのように非常に規則的な入力形式を必要とする．
点群やメッシュは不規則なデータであるため，多くの研究者は，ネットワークに送る前にボクセルや画像集合のデータに変換する．
しかし，このデータ形式の変換は，結果データを不必要に膨大にさせたり，アーティファクトを発生させてしまう．
このような理由から，点群を使用する，別の３次元幾何形状の入力形式に焦点をあてる．そして，このディープネットワークを「PointNet」と命名する．
点群は，組み合わせの不規則さやメッシュの複雑さを回避する，シンプルかつ統一された構造であるため，学習が容易．
しかしながらPointNetは，点群は単なる点の集合であるため点の順番は不変である，という事実に配慮する必要があり，ネットワーク計算において，ある程度の対称化が必要となる．
PointNetは，点群を入力として直接使用し，入力全体に対するクラスラベル，あるいは入力の各点に対する部分ラベルを出力とする，統一されたアーキテクチャである．
PointNetの初期段階では，各点が等しく独立に処理されるため，非常にシンプルな構造である．
基本設定では，各点は単に $(x, y, z)$ の３つの座標で表現される．
法線や他のローカルまたはグローバル特徴量などの追加の次元が追加されても問題ない．
PointNetの重要なカギは，単一の対称性関数，最大プーリングの使用である．
ネットワークは，点群の有益な点を選択し，選択された理由を符号化する一組の最適化関数を効率的に学習する．
ネットワークの全結合層は，学習済み最適値を全体形状のためのグローバル記述子に集約するか（形状分類），あるいは点ラベルごとに予測することに使用される（形状分割）．
PointNetの入力形式は，各点を独立に変換するため，剛体変換またはアフィン変換を適用するのが容易．
したがって，PointNetが処理をおこなう前に，データの正規化を試みるデータ依存空間変換ネットワークを追加することで，結果をさらに改善することができる．
PointNetの理論的分析と実験評価をおこなう．
PointNetは任意の連続関数に近似することができる．
さらに興味深いことに，PointNetはスパースな一連のキー点によって，入力点群を要約することを学習する．
これは，オブジェクトの概形を可視化することに相当する．
理論的分析は，なぜPointNetが入力点群の小さい摂動や外れ値，欠損に対してロバストであるかを明らかにする．
形状分類，部分分割，シーン分割など様々なベンチマークデータセットについて，最先端の手法とPointNetとの比較実験をおこなう．
統一されたアーキテクチャの状況下では，PointNetははるかに高速であるだけでなく，最先端と同等あるいはそれ以上の強力なパフォーマンスを発揮する．
本研究の主な貢献は，以下の通りである：
- 無秩序な３次元点の集合に適した，新しいディープネットワークアーキテクチャの設計；
- PointNetがどのように３次元形状を学習するかの証明；
- 経験的，理論的分析を通した，PointNetの安定性と効率性の証明；
- ニューロンによって計算される３次元特徴の図示と，性能に関する直感的な説明；
ニューラルネットワークによる無秩序なセットの処理の問題は，非常に一般的かつ根本的な問題である．
本研究のアイデアが，他の分野にも応用されることに期待している．

f:id:tom0930:20190510002327p:plain — Figure 1.

2. Related Work

Point Cloud Feature

点群における既存のほとんどの特徴は，特定のタスク向けに手作りされている．
点の特徴はしばしば，点群の特定の統計的な特性を変換し，特定の変換に対して不変であるように設計されている．
点の特徴は，local features と global features に分類される．
特定のタスクにおいて，最適な特徴の組み合わせを探すことは簡単ではない．

Deep Learning on 3D Data

3Dデータには，学習のための様々なアプローチに至る複数の表現形式がある．
Volumetric CNN は，ボクセル化された形状にCNNを適用する手法です．
しかし，ボクセル表現は，データのスパース性と3次元の畳み込みの計算コストのために，解像度の制約を受ける．
FPNN と Vote3D は，スパース性の問題に対処するための特別な手法を提案した．
しかし，それらの操作は，スパース点群に対しておこなわれるため，大規模点群に適用することは困難．
Multiview CNN は，3次元点群を2次元画像にレンダリングし，2次元のCNNを適用することを試みた．
よく設計された2次元CNNを用いて，Multiview CNN は優れた性能を発揮した．
しかし，シーンの理解や，点分類や形状補間などの他の3次元タスクに応用することは困難である．
Feature-based DNNs は，まず従来の形状特徴を抽出することによって3次元データをベクトルに変換し，その後に形状を分類するために全結合層を使用する．
しかし，抽出された特徴の表現力に制約されてしまう可能性がある．

Deep Learning on Unordered Sets

データ構造の観点からすると，点群は順不同（順序付けられていない）ベクトルの集合である．
Oriol Vinyals らは最近この問題について調査した．
しかし，彼らはNLPに焦点を当てているため，集合における幾何学の役割が欠如している．

3. Problem Statement

我々は，入力として，順序付けされていない点群を直接使用するフレームワークを設計する．
点群は3次元的な点の集合として表現される．各点 $P_i$ はベクトル $(x, y, z)$ で，追加次元として色や法線のような特徴チャンネルを含む．
便宜上，特に明記しない限り、 $(x, y, z)$ 座標のみをポイントのチャンネルとして使用する．
オブジェクト分類タスクに関しては，入力点群は，形状から直接サンプリングされるか，またはシーン点群から事前にセグメントされる．
PointNetは， $k$ 個のすべての候補について， $k$ 個の点数を出力する．
意味分割に関しては，入力点群は，部分領域セグメンテーションのための単一オブジェクト，またはオブジェクト領域セグメンテーションのための3次元シーンからのサブボリュームである．
$n$ 個の点と $m$ 個の意味付けサブカテゴリーのそれぞれについて， $n×m$ 個の点数を出力する．

4. Deep Learning on Point Sets

PointNetの構造(4.2節)は， $\mathbb{R}^{n}$ (4.1節)における点集合の性質にインスパイアされている．

4.1 Properties of Point Sets in $\mathbb{R}^{n}$

入力は，ユークリッド空間における点の集合であり，以下の3つの主な性質を持っている．
- 順不同．画像におけるピクセル配列や，ボクセルグリッドにおけるボクセル配列とは異なり，点群は特定の順序がない点の集合である．言い換えると， $N$ 個の点を有する3次元点群を入力とするネットワークは，入力点順に設定された $N!$ の順列に対して不変である必要がある．
- 点間の相互作用．点は，距離空間に存在しているため孤立しておらず，近傍点が意味のあるサブセットを形成する．それゆえ，モデルは，近傍点から局所構造，および局所構造間の組み合わせ相互作用を検知可能である必要がある．
- 変換に対する不変性．幾何学オブジェクトに関して，学習された点集合の表現は，特定の変換処理に対して不変である必要がある．例えば，点群全体を回転させたり並進させたとしても，globalな点のカテゴリーや点の分割は変更されてはいけない．

4.2 PointNet Architecture

PointNetのネットワーク構造を Fig2. に示す．
classification networkとsegmentation networkは，大部分を共有している．
Pipeline：
- classification networkは入力として $n$ 点を受け取り，入力変換と特徴変換を適用したのち，max pooling を使用して特徴点を集約する．出力は $k$ 個のクラスに対する分類スコアとなる．
- segmentation networkは，classification networkの拡張版であり， global features と local feature を連結し，点ごとのスコアを出力する．
- "mlp"は，"multi-layer perceptron"意味しており，()内の数は各層のサイズである．
- Batchnormは，ReLUが適用されるすべての層に使用される．
- Dropout layers は，classification network の最後の mlp に使用される．

f:id:tom0930:20190513200909p:plain — Figure 2.

PointNetには，３つの重要なモジュールがある：
- max pooling layer（すべての点の情報を集約するための対称関数として）
- a local and global information combination structure
- two joint alignment networks that align both input and point features
以降で，それぞれについて説明する．

Symmetry Function for Unordered Input

モデルを入力に対して順不同にするには，3つの方法がある：
1. 入力を標準的な順番にソートする
2. 入力の順序を定める（すべての順列を考慮する必要があり，トレーニングデータが増大する）
3. 各点の情報を集約するために単純な対称関数を使う（対称関数は，入力として $n$ 個のベクトルを取り，入力順序に不変な新しいベクトルを出力する．例えば，+や*などの演算子は，対称二項関数である．）
ソートは単純な解決作のように思えるが，高次元空間において，点の摂動に関して安定な順序は実際には存在しない．
したがって，ソートでは順序付け問題を完全に解決できず，順序付け問題が存在する限り，入力から出力の一貫したマッピングを学習することは困難である．
Fig5. に示すように，ソートされた点集合に対して直接 MLP を適用すると，ソートしていない点集合を直接処理するよりわずかに優れているものの，不十分なパフォーマンス結果であった．（accuracy：24.2→45.0）

f:id:tom0930:20190515233055p:plain — Figure 5.

我々のアイデアは，集合内の要素に対称関数を適用することによって，点集合で定義された関数を近似することである：

f:id:tom0930:20190515234252p:plain

経験的に，我々の基本的なモジュールは非常に単純である：
MLP によって $h$ を近似し，一変数関数と Max pooling 関数の合成によって $g$ を近似する．
この方法は，実験によってうまくいくことがわかった．
この重要なモジュールは単純なように思えるが，興味深い特性がある（Sec 5.3）．
また，いくつかの異なるアプリケーションにおいて，強力なパフォーマンスを発揮する（Sec 5.1）．
このモジュールの単純さのおかげで，Sec4.3 において理論的な分析をおこなうことができる．

Local and Global Information Aggregation

上記のセクションからの出力は，入力集合の global signature である，ベクトル $[f_1, \ldots , f_K$ ] を形成する．
classification においては，shape global feature について，SVM や MLP を容易に訓練することができる．
しかし，segmentation においては，local と global の情報の組み合わせが必要となる．
我々は，シンプルではあるが非常に効果的な方法で，これを実現することができる．

われわれの解決策は Fig2. の Segmentation Network である．
global point cloud feature ベクトルを計算後に，global feature を各点の feature と連結することによって，点ごとの features にフィードバックする．
それから，連結された point features に基づいた，点ごとの features を抽出する．
このときに，点ごとの feature が， local と global の情報を認識する．

この修正によって，PointNet は点ごとに，local geometry と global semantics の両方に依存する量を予測することができる．
例えば，次の図に示すように，点ごとの法線を正確に予測することができる：

f:id:tom0930:20190517205759p:plain — Normal Reconstruction Results

この結果から，ネットワークが点の local neighborhood の情報を認識可能であるということが確認できる．
検証実験のセッションでは，PointNet が，shape part segmetation と scene segmentation に関して，最先端の性能を達成できることを示す．