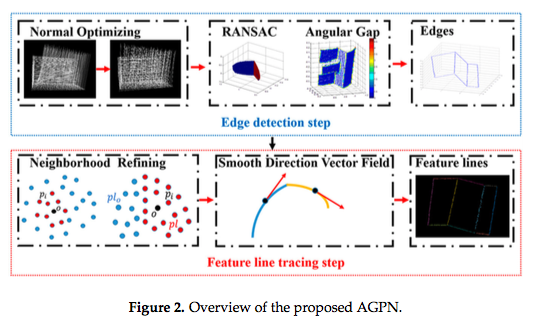
Edge Detection and Feature Line Tracing in 3D-Point Clouds by Analyzing Geometric Properties of Neighborhoods

Paper（13000 words，Remote Sens. 2016）

www.semanticscholar.org

Abstract

• 本論文では，3次元点群データからエッジを抽出し，特徴線をトレースする，自動化された効果的な手法を提案する．
• この手法は，Analysis Geometric Properties of Neighborhoods（AGPN）と呼ぶ．
• AGPNは，エッジ抽出と特徴線のトレースの2つのステップを含んでいる．
• エッジ抽出ステップでは，AGPNが注目点の近傍点の幾何学的特性を分析し，RANSACとangular gap metricを組み合わせてエッジ抽出を行う．
• 特徴線トレースステップでは，検出されたエッジ領域の拡大とモデルフィッティングに基づくハイブリッドな手法によって，特徴線がトレースされる．
• 我々の手法は，複雑な人工物や数百万点の大規模都市シーンにおいて有効である．
• さらに，AGPNは入力点群の点密度に影響されない(insensitive)．

1. Introduction

1.1 Problem Statement

• 近年のセンサー技術やレーザ計測技術の発達により，内容が高密度で理解しにくい(dense)3次元点群が一般的になってきた．
• それゆえ，3次元点群におけるエッジ抽出や特徴線抽出が，新たな(novel)研究トピックになってきている．
  
  

• 画像に対してはある程度確立されたエッジ抽出手法は，以下の3つの理由から，3次元点群に対して直接適用することはできない．

1. データの記述方法が異なる．
   画像は，行と列で考えることができるが，3次元点群は非構造型で非一様な分布である．
2. 表現される情報の種類が異なる．
   画像は，非明示的な空間情報と十分なスペクトラム情報を含む．それに対して，3次元点群は明白な空間情報を含む．
3. 空間的な近傍が異なる．
   画像はグリッドのように整列されており，ピクセルの近傍を容易に決定することができる．しかしながら，3次元点群は非構造型であり，点の近傍は画像のピクセルよりも複雑である．一般的に，3次元点群において球面近傍，円柱近傍，k近傍の3種類の近傍が存在する．3種類の近傍は，異なる探索手法に基づいており，探索手法に応じて近傍は異なる．
   
   

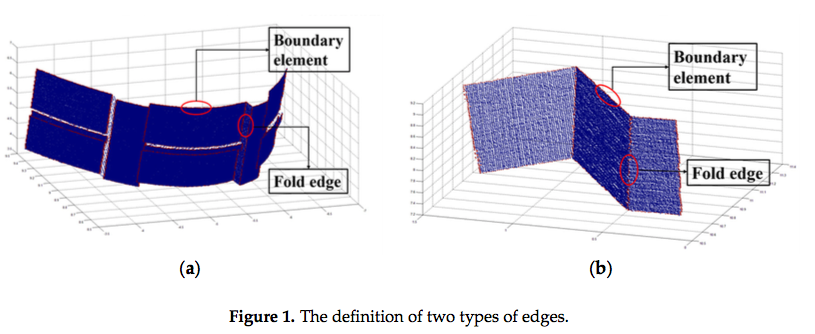
• 数学的には，3次元エッジをBoundary elementsとFold Edgesの2種類に定義する．

1. 近傍によって形成された形における角度の急な変化に関連する境界要素(Boundary elements)．Boundary elementsは，輪郭部分に現れる．特に，表面は，3次元平面や曲面である．
2. 隣接する表面における法線ベクトル間の，急な方向の変化(Fold edges)．Fold edgesは，平面が交差する線(稜線)や尖った特徴線など異なるサーフェス間の交差部分に現れる．

• 3次元点群に対するエッジ抽出は，2次元画像処理と似ている．
• エッジ抽出は2つのステージから構成される．
  (1) 元画像を特徴量に変換する．
  (2) 各点をエッジ部と非エッジ部に分ける．
• 同様にして，提案エッジ抽出手法は最初に各点に対してangular gap featureを計算し，それから，各点をエッジ部と非エッジ部に分類する．
• 場合によっては，輪郭を取得するために一度検出されたエッジをさらにテストする，エッジリンキングと呼ばれるステージがある．
• 本論文では，抽出したエッジを境界や交差線のような特徴線と紐付けるために，特徴線トレーシングを提案する．

1.2 Related Work

4. Conclusions

• 本論文では，3次元点群からエッジを抽出し特徴線をトレースする，AGPNと呼ばれる自動かつ効率的な手法を提案した．
• AGPNは，エッジ抽出と特徴線トレースの2つのステップで構成されている．
• 最初のステップでは，注目点の近傍の幾何学的特性を分析し，RANSACと注目点をエッジかどうかラベル付けするためのangular gap criterionを組み合わせる．
• 次のステップでは，AGPNは抽出されたエッジに対して特徴線をトレースする．
• AGPNの貢献は，以下の3つである．
  (1) セグメンテーションやプリプロセスのような前処理を必要としない．
  (2) 定義されたすべての3次元エッジを抽出可能で，ノイズの影響を受けない．
  (3) AGPNの特徴線トレースステップは，複雑な近傍ににおける空間的に隣接する共線状，同軸状の線を分類するのに利用される．
• しかし，特徴線トレース処理のパラメータが厳密であるか，特徴線においてギャップがある場合に，過分類が生じる可能性がある．
• 将来的には，提案手法を大規模3次元点群における物体認識に適用したい．

3. Experiments and Analysis

• 提案したアルゴリズムは，PCLを用いてC++で実装された．
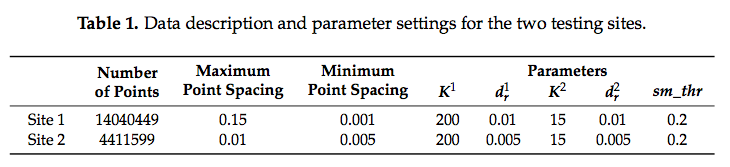
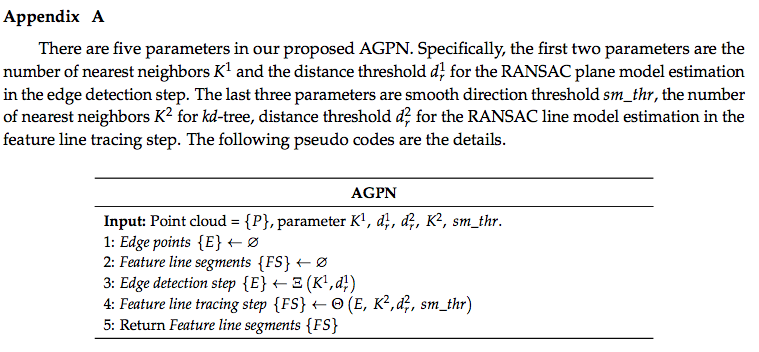
• AGPNには5つのパラメータがある．
• 入力点群の点間隔が，AGPNのパフォーマンスに影響を及ぼす．
• さらに，点間隔に関係する距離閾値パラメータdr1，dr2も影響を受ける．
• セクション3.1でテストデータについて，セクション3.3でパラメータチューニングについて記述する．
• 提案手法を定量的に評価するために，セクション3.2で4つの計測を定義する．
• さらに，提案手法を既存の代表的な2つのアルゴリズムと比較する．
• 1つは，PCLの境界予測手法．もう1つは，参考文献[13]で提案されているエッジ点クラスタリングアルゴリズムである．
• これらの比較については，セクション3.7に記述されている．

3.1 Testing Data

• テストデータは，3DTK - The 3D Toolkitから，Site1，Site2の2つを選択した．
• 点密度は，非一様である．
• 2つのデータセットに関する詳細な情報をTable 1.に示す．
• 2つのテストデータは，点間隔がまったく異なる．
• Site1は点密度が非一様．計測器に近い位置では，平均点間隔は0.001m．計測器から離れた位置では，平均点間隔は0.15m．
  → 計測器から遠いほど，点密度が小さい．

3.2 Evaluation Metrics

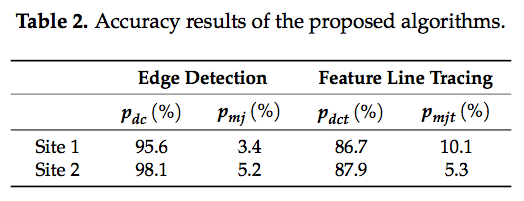
• エッジ抽出ステップと特徴線トレースステップを定量的に評価するために，それぞれ4つの基準で評価する．（式(5)〜(8)）
• Pdc，Pmjは，それぞれエッジ抽出ステップの正確率，非正解率．
• Pdct，Pmjtは，それぞれ特徴線トレースステップの正確率，非正解率．

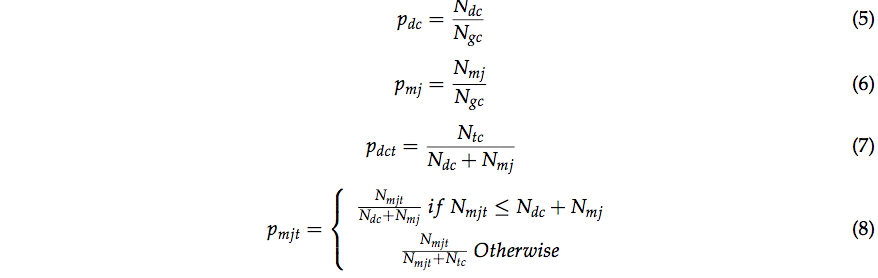
• Ndcは，抽出されたエッジのうち，正解の特徴線の数．
• Ntcは，特徴線トレースステップにおいて，正確にトレースされた特徴線の数．
• Ngcは，ground truth内の特徴線の合計の数．
• Nmjは，抽出されたエッジのうち，非正解の特徴線の数．
• Nmjtは，特徴線トレースステップにおいて，非正確にトレースされた特徴線の数．
• PdcとPdctの値が大きく，PmjとPmjtの値が小さいほど，より望ましい．

3.3 Parameter Tuning

• K1とK2は結果にほとんど影響を与えないため，Site1とSite2に対してK1=200，K2=15を維持した．
• 特徴線トレースパラメータは，ユーザの要求に依存するため，3D線分抽出の適用に対する影響のみを分析する．この条件下では，結果の十分な質を保証するために，sm_thrは0.2に設定する．
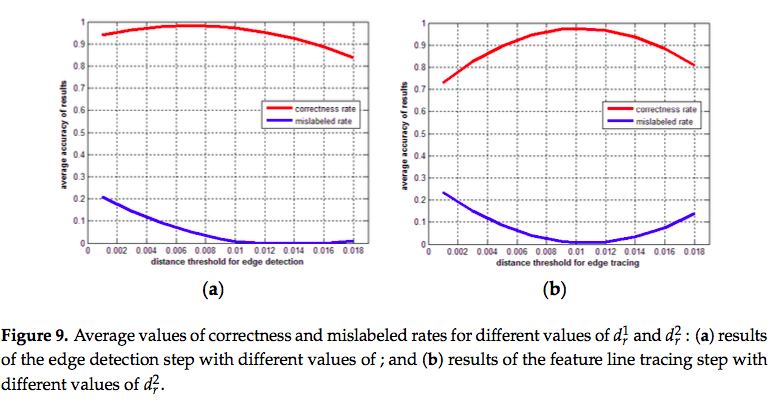
• Figure 9.によれば，入力点群の点間隔が均一であれば，入力点群の点間隔と等しいdr1，dr2（合理的な構成）が得られる． 
• 入力点群の点間隔が不均一であれば，点密度の傾向に応じて，パラメータを設定することができる．

3.4 Normal Estimation

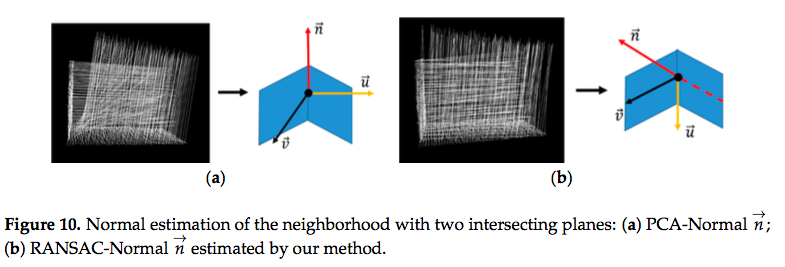
• RANSAC-Normalの実現可能性を実証するために，PCA-Normalと比較する．
• PCA-Normalは，交差する2つの平面のいずれかに直行するよりもむしろ，接平面に対して直交している．（Figure 10a）
• RANSAC-Normalは，交差する2つの平面のいずれかに直交する．（Figure 10b）
• RANSAC-Normalであれば，推定した法線を基に平面に沿ったベクトルを計算することができるため，提案手法の要求を満たす．

3.5 Influence of Point Density

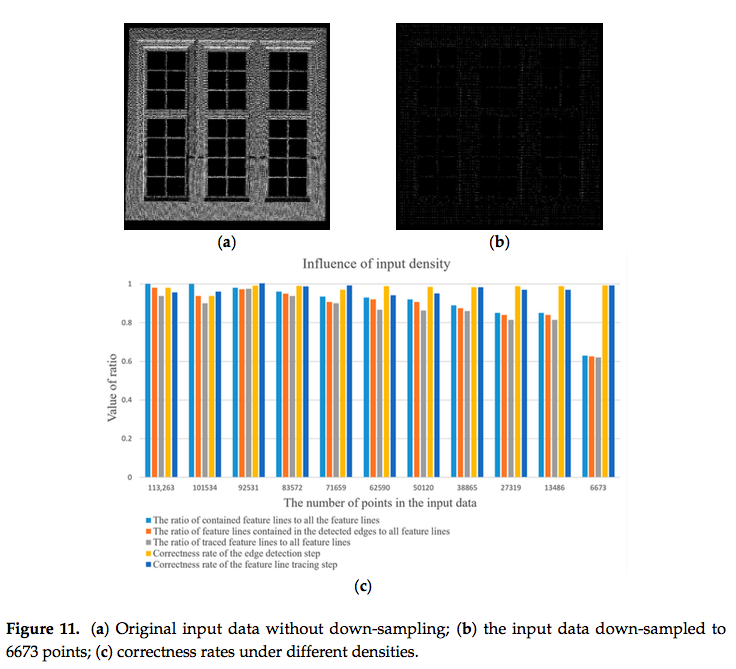
• 入力点群の点密度は主に，複雑なオブジェクトの細部を決める．
• 入力点群の点密度の，エッジ抽出ステップと特徴線トレーシングステップの結果への影響を分析するために，異なる点密度のwindowの点群データ（Figure 11a）に対して，ダウンサンプリングを行った．
• Figure 11cのx軸は，グラフダウンサンプリングによって間引いた点の数．
• この実験から，入力点群データに特徴線が含まれている限り，我々の手法は，エッジを抽出し特徴線セグメントをトレースすることが可能であることがわかる．
• したがって，エッジ抽出ステップと特徴線トレーシングステップの精度が点密度に影響されないということを，実験結果が証明している．

3.6 Results

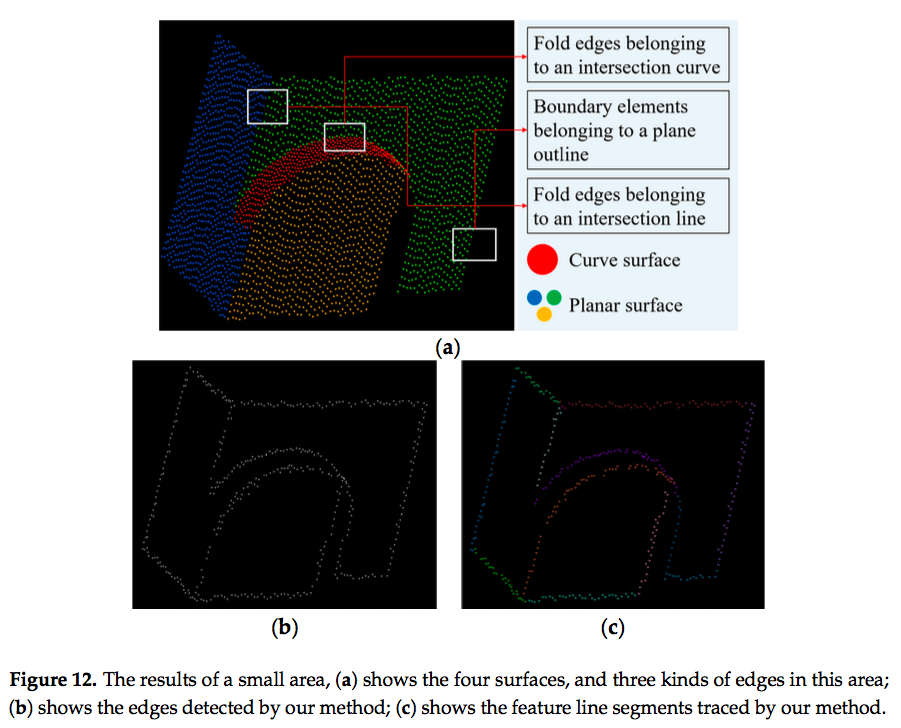
• Figure 12.において，Curve surfaceは赤，3つのPlanar surfaceは青，緑，黄色で色付けされている．
• また，3種類のエッジが白い四角形でマーキングされている．
• 提案手法であるAGPNの適用結果をFigure 12b, cに示す．bが抽出したエッジを示している．cは異なる色で色付けされてトレースされた特徴線を示している．

3.7 Comparative Studies

• 既存の手法とAGPNの2つのステップを別々に比較する．
• 提案したエッジ抽出手法とPCLで提案されている境界推定手法との比較結果をFigure 15.に示す．
• 提案手法は，オブジェクトの複雑さに関係なく，全ての種類のエッジを抽出できている．
• 一方，PCLの手法は，Fold edgesを抽出することができていない．
• 提案手法とPCLの精度の比較をTable 3に示す．

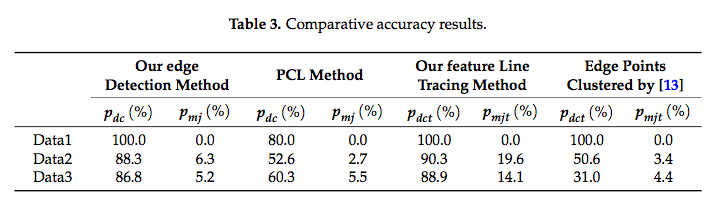
• PCLの手法は，angle criterionのみを利用してエッジを抽出するため，fold edgesを抽出するのに不十分である．
• 加えて，外れ値やノイズの影響を無視して，PCAによる法線推定を利用して境界面を抽出している．
• したがって，PCLの手法は，複雑な近傍を含むエッジを扱うことができない．

2. Methodology

2.1 Overview

2.2 Edge Detection

　2.2.1 Geometric Property Analysis

• エッジであることの特性は，点自身ではなく，点の近傍．
  → 点自身を見ても意味がなく，点の近傍を見る必要．
• この原則に基づき，注目点の近傍の幾何学的特性を分析することにより，注目点がエッジかどうかを決定するアルゴリズムを設計する．
• AGPNのエッジ抽出ステップのフローチャートをFigure 3.に示す．

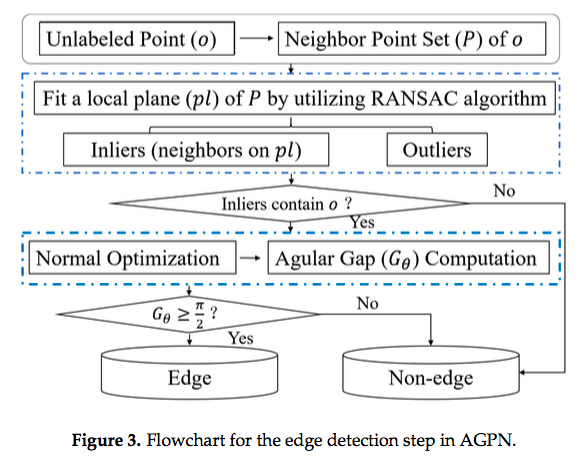
• 点oは，ラベル付けされてない点とする(denote)．
• まず最初に，距離に基づいて点oの近傍点集合Pを探索する．
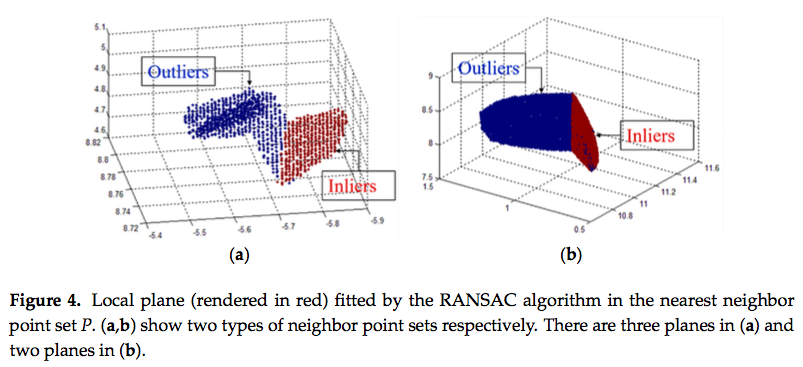
• 次に，RANSACによって，近傍点集合Pを局所平面plに適合させる．それから，Pをinliers(pl上の点群)とoutliersに分類する．
• 点oが，inliersに分類されなかった場合，非エッジ点としてラベル付けする．
• 点oが，inliersに分類された場合，点oとinliersを多数の空間ベクトルを構成するために接続する．そこから，最適化された法線ベクトルに基づきangular gapを計算する（セクション2.2.4）．
• 平面pl上に構成された空間ベクトル間に十分なangular gapが存在する場合，点oをエッジ点としてラベル付けする．
• 平面pl上に構成された空間ベクトル間に十分なangular gapが存在しない場合，点oを非エッジ点としてラベル付けする．
• すべての点に対してラベル付けしたあと，エッジが検出される．
• 点oが平面外縁部上または平面の交線上にある場合，平面のモデルフィッティングは完璧．
• 点oが曲面境界上または異なる曲面の交線上にある場合，平面のモデルフィッティングであっても，局所的なスムーズ表面を予測するのに効果的である．なぜならば，点oの近傍は，小さな局所領域だからである．
• RANSACによってフィッティングされた平面モデルに基づいて，近傍点集合Pはinliersとoutliersに分類される．（Figure 4.）
• AGPNのエッジ抽出手順では，境界要素(外縁部)と稜線の両方を抽出することができる．（セクション2.2.2 & 2.2.3）

　2.2.2 Boundary Element Detection

• Figure 5.に示すように，ラベル付けされてない点oの近傍には，表面は1つだけ存在する．

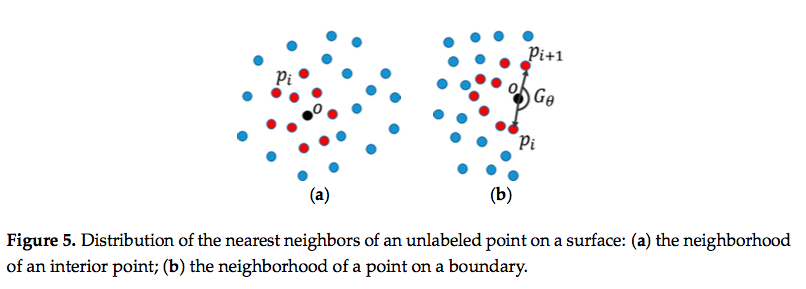
• 青と赤で色付けされたK個の点は，kd-treeを用いて取得された点oの近傍点である．
• 赤色で色付けされた点集合Piは，RANSACによって抽出されたinliersである．これらのinliersは，フィッティングされた局所表面の平面pl上にある．
• 点oが境界付近上にある場合（Figure 5b），局所平面pl上のベクトルopi間のangular gap Gθは十分にある．
• 点oが内部にある場合（Figure 5a），十分なagular gapはない．

　2.2.3 Fold Edge Detection

　2.2.4 Normal Optimization

　2.2.5 Angular Gap Computation

2.3 Feature Line Tracing

　2.3.1 Neighborhood Refinement

• 画像と比較して，3次元点群は非構造で点が散乱しているため，エッジ点群の近傍探索が困難である．
• 提案手法は，最初にkd-treeを用いて注目点の近傍点群を取得する．
• 次に，直線モデルをRANSACによって適合させる．
• それから，近傍点群がinliersとoutliersに分類される．
• 注目点を含むinliersは，修正された近傍点群である．
• outliersは，アップデートしたinliersが注目点を含むまでRANSACによって繰り返し処理される．
• それゆえ，適応近傍は書く注目点に対して設計されている．

　2.3.2 Growing Criterion Definition

• 本研究では，参考文献[46]によって与えられる2つのgrowing criteriaを再定義する．

1. Proximity of points(点の近似)．現在のセグメント内の点群の1つに近い点のみが，現在のセグメントのスタックに追加される．特徴線トレーシングのおいて，このエッジ点の近似は，セクション2.3.1のNeighborhood refinementによって実現できる．
2. Smooth direction vector field(滑らかな方向ベクトルフィールド).現在のトレーシングセグメントと同様の主成分方向を持つ点のみが，現在のセグメントのスタックに追加される．本研究では，直線モデルが最初にRANSACによってアップデートされた近傍点に対して適合される．それから，現在の点の主成分方向が，適合された直線の方向として定義される．

• さらに，近傍点に対してinliersの割合が高いことは，特徴線の未決の可能性が高いことを意味する．
• 領域拡大手順は不可逆的であるため，線形性が高いエッジ点から先に処理して，良い結果を確保しておく必要がある．
• それゆえ，エッジ点群を最初にそれぞれの比率値によってソートしてから，順番に処理する．
• 線形的な特徴セグメントに対する一般的な領域拡大手順は，初期点の位置や局所近傍点のサイズに敏感である．
• しかし，前述のように近傍のアップデートやエッジ点群のソートを行うことで，この問題を回避することができる．
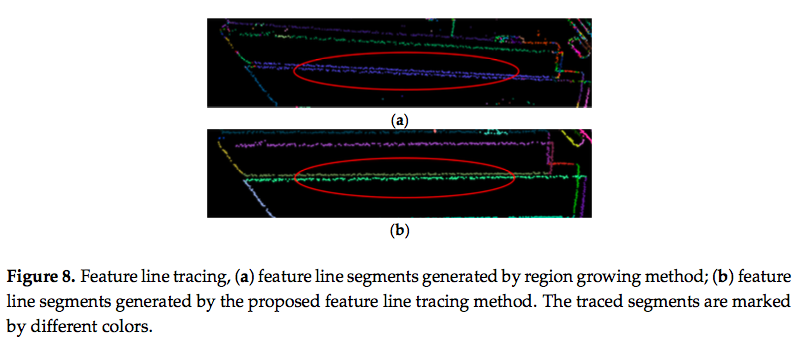
• 提案した特徴線トレーシング処理では，空間的に隣接した同一線や同一軸線を区別することができる．（Figure 8）

• 特徴線トレーシングステップでは，3つのパラメータが使われる．
• 近傍点群の数K2(kd-treeのため)，距離閾値dr2(RANSACによる直線モデル推定のため)，スムーズ方向閾値sm_thr．
• トレースした特徴線をFigure 8bに示す．