基底変換 対角化

数学

f:id:tom0930:20180529172333p:plain

基底変換の様子

 

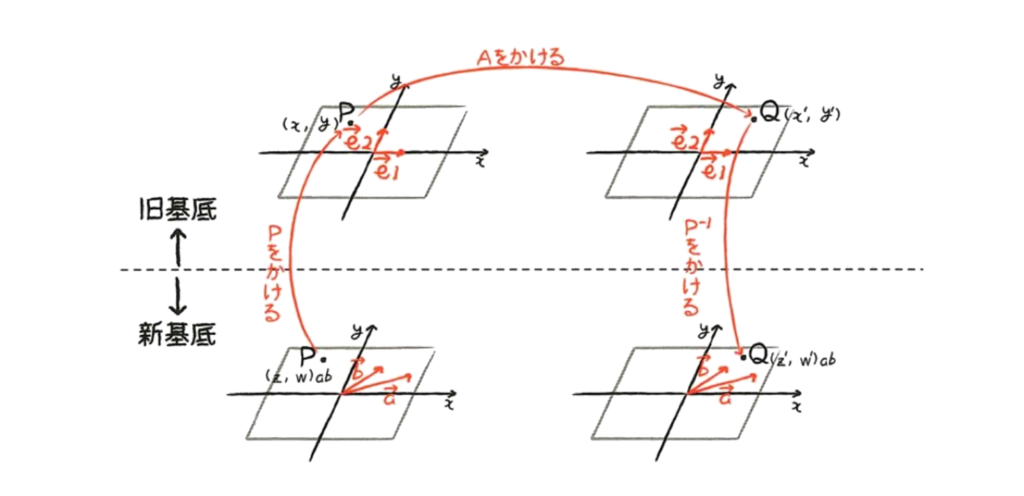
  • ある基底（都合の悪い基底）で，$ \left( \begin{array}{c} x\\ y\\ \end{array} \right) $という座標が与えられているとする．
  • 行列$A$をかけて，$ \left( \begin{array}{c} x\\ y\\ \end{array} \right) $が座標変換された先の座標$ \left( \begin{array}{c} u\\ v\\ \end{array} \right) $を求めたいとする．
  • 座標変換前の座標が$ \left( \begin{array}{c} x\\ y\\ \end{array} \right) $，
    座標変換後の座標が$ \left( \begin{array}{c} u\\ v\\ \end{array} \right) $である．
  • すると，以下の式で表せる：
    \begin{equation}
    \left(
    \begin{array}{c}
    u\\
    v\\
    \end{array}
    \right)
    = A
    \left(
    \begin{array}{c}
    x\\
    y\\
    \end{array}
    \right)
    \end{equation}．
  • しかし，このままでは基底のとり方が悪いため，そのまま計算はしたくない．
  • そこで，基底変換行列$P$をかけて，座標$ \left( \begin{array}{c} u\\ v\\ \end{array} \right) $を都合の良い基底に変換することを考える．
    つまり，式(1)に対して，両辺左から行列$P$をかければよい．
  • すると，以下の式のようになる：
    \begin{equation}
    P
    \left(
    \begin{array}{c}
    u\\
    v\\
    \end{array}
    \right)
    =
    P
    A
    \left(
    \begin{array}{c}
    x\\
    y\\
    \end{array}
    \right)
    \end{equation}．
  • しかし，これでは，式(2)の右辺を見ればわかるように，
    座標$
    \left(
    \begin{array}{c}
    x\\
    y\\
    \end{array}
    \right)
    $を都合の良い基底に変換できていない．
  • そこで，$ P^{-1}P=E $であるから，式(2)は以下のように表しても問題ない：
    \begin{equation}
    P
    \left(
    \begin{array}{c}
    u\\
    v\\
    \end{array}
    \right)
    =
    P
    A
    P^{-1}
    P
    \left(
    \begin{array}{c}
    x\\
    y\\
    \end{array}
    \right)
    \end{equation}．
  • これで，両座標とも，都合の良い基底に変換される．
  • ここで，都合の良い基底に変換されたあとの両座標を
    \begin{equation}
    \left(
    \begin{array}{c}
    u'\\
    v'\\
    \end{array}
    \right)
    =
    P
    \left(
    \begin{array}{c}
    u\\
    v\\
    \end{array}
    \right)
    ，
    \left(
    \begin{array}{c}
    x'\\
    y'\\
    \end{array}
    \right)
    =
    P
    \left(
    \begin{array}{c}
    x\\
    y\\
    \end{array}
    \right)
    \end{equation}
    とおく．
  • 式(4)を用いると，式(3)は以下のようになる：
    \begin{equation}
    \left(
    \begin{array}{c}
    u'\\
    v'\\
    \end{array}
    \right)
    =
    P
    A
    P^{-1}
    \left(
    \begin{array}{c}
    x'\\
    y'\\
    \end{array}
    \right)
    \end{equation}．
  • 式(5)において，$PAP^{-1}$は，行列$A$の固有値(ここでは，$eigenvalue_A$と表記する)を並べて以下のように対角化できる：
    \begin{equation}
    P
    A
    P^{-1}
    =
    \left(
    \begin{array}{cc}
    eigenvalue_A & 0\\
    0 & eigenvalue_A
    \end{array}
    \right)
    \end{equation}．
  • 以上より，式(6)を式(5)に代入して，最終的に以下の式が得られる：
    \begin{equation}
    \left(
    \begin{array}{c}
    u'\\
    v'\\
    \end{array}
    \right)
    =
    \left(
    \begin{array}{cc}
    eigenvalue_A & 0\\
    0 & eigenvalue_A
    \end{array}
    \right)
    \left(
    \begin{array}{c}
    x'\\
    y'\\
    \end{array}
    \right)
    \end{equation}．
  • 式(7)は，都合の良い基底であるため，$
    \left(
    \begin{array}{c}
    u'\\
    v'\\
    \end{array}
    \right) $ は容易に求めることができる．
  • あとは，都合の良い基底で求まった座標$\left(
    \begin{array}{c}
    u'\\
    v'\\
    \end{array}
    \right) $を元の基底（都合が悪かった基底）での座標に戻してやれば，最初に求めたかった座標がわかる．